Neil K. Dhingra – Ph.D. Thesis

Optimization and control of large-scale networked systems

Neil K. Dhingra, University of Minnesota, Twin Cities

Abstract

In this thesis, we design structured controllers for linear systems by solving regularized optimal control problems. We develop tractable methods for solving nonconvex regularized problems and then identify classes of problems for which regularized optimal control problems can be placed into a convex form.

We first develop novel methods based on reformulating the regularized optimization problem with an auxiliary variable. By exploiting the properties of proximal operators, we bring the associated augmented Lagrangian into a continuously differentiable form by constraining it to the manifold that corresponds to explicit minimization over the auxiliary variable. The new expression facilitates a method of multipliers algorithm that offers many advantages relative to existing methods, including guaranteed convergence for nonconvex problems and the ability to impose regularization in alternate coordinates. We then apply primal-descent dual-ascent Arrow-Hurwicz-Uzawa type gradient flow dynamics to solve regularized problems in a distributed manner. We prove global convergence for convex problems and use the theory of Integral Quadratic Constraints to establish conditions for exponential convergence for continuous- and discrete-time updates applied to strongly convex probems. Finally, we take advantage of generalizations of the Jacobian to develop a second-order algorithm which converges globally to the optimal solution for convex problems. Moreover, we prove local quadratic convergence for strongly convex problems.

We next study several classes of convex regularized optimal control problems. The problem of designing symmetric modifications to symmetric linear systems is convex in the underlying design variable and is thus appealing for the purpose of structured control. We show that even when the system and controller are not symmetric, their symmetric components can be used to perform structured design with stability and performance guarantees. We then examine the problem of designing structured diagonal modifications to positive systems. We prove convexity of the 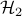and 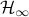optimal control problems for this class of system and apply our results to leader selection in directed consensus networks and combination drug therapy design for HIV. We consider time-varying controllers and show that a constant controller is optimal for an induced-power performance index. Finally, we develop customized algorithms for large-scale actuator and sensor selection